Note
Go to the end to download the full example code.
SKADA logo generation
In this example we plot the logos of the SKADA toolbox.
This logo is that it is done 100% in Python and generated using matplotlib and plotting the solution of the EMD solver from POT.
# Author: Théo Gnassounou
#
# License: BSD 3-Clause
# sphinx_gallery_thumbnail_number = 1
from math import factorial
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams.update({"text.usetex": True, "font.family": "Computer Modern"})
color_S = "black"
color_1 = "#2364aa"
color_0 = "#c84630"
color_unlabel = "#999c81"
def comb(n, k):
return factorial(n) // (factorial(k) * factorial(n - k))
def bezier_curve(t, points):
n = len(points) - 1
return sum(comb(n, i) * (1 - t) ** (n - i) * t**i * points[i] for i in range(n + 1))
def draw_S(
start_length=9,
length_step=2.5,
final_angle=70,
angle_step=18,
s=30,
alpha=0.9,
linewidths=1,
random_state=42,
figsize=(2, 2),
white=False,
):
rng = np.random.RandomState(random_state)
# Create a figure and axis
fig = plt.figure(1, figsize)
if figsize == (2, 2):
plt.xlim(-1, 11)
else:
plt.xlim(-1, 35)
# Define the control points for the Bézier curve
points = np.array([[2, 8], [4, 10], [6, 0], [8, 2]])
# Generate the S shape
t_values = np.linspace(-0.3, 1.3, 100)
curve = np.array([bezier_curve(t, points) for t in t_values])
for i, angle in enumerate(range(0, final_angle, angle_step)):
rotation_center = np.mean(curve, axis=0)
rotation_angle = np.radians(angle)
rotation_matrix = np.array(
[
[np.cos(rotation_angle), -np.sin(rotation_angle)],
[np.sin(rotation_angle), np.cos(rotation_angle)],
]
)
rotated_curve = (
np.dot(curve - rotation_center, rotation_matrix) + rotation_center
)
# Plot the S shape
plt.plot(
rotated_curve[:, 1],
rotated_curve[:, 0],
color=color_S if not white else "w",
linewidth=start_length - length_step * i,
alpha=1 - i / (final_angle / angle_step),
solid_capstyle="round",
)
# Plot the S shape
plt.plot(
curve[:, 1],
curve[:, 0],
color=color_S if not white else "w",
linewidth=2,
solid_capstyle="round",
)
n_dots = 200
max = 2
min = 1
dots = rng.rand(n_dots, 2) * 10
dots_class = []
dots_keep = []
for i, dot in enumerate(dots):
# get the closest x axis point of the curve of dot
closest_point = curve[np.argmin(np.abs(curve[:, 0] - dot[0]))]
if (abs(closest_point[1] - dot[1]) < max) & (
abs(closest_point[1] - dot[1]) > min
):
dots_keep.append(dot)
if closest_point[1] > dot[1]:
dots_class.append(1)
else:
dots_class.append(0)
dots_keep = np.array(dots_keep)
dots_class = np.array(dots_class)
plt.scatter(
dots_keep[dots_class == 0, 1],
dots_keep[dots_class == 0, 0],
color=color_unlabel if not white else "w",
marker="o",
s=s,
alpha=alpha,
linewidths=linewidths,
)
plt.scatter(
dots_keep[dots_class == 1, 1],
dots_keep[dots_class == 1, 0],
color=color_unlabel if not white else "w",
marker="s",
s=s,
alpha=alpha,
linewidths=linewidths,
)
dots_rotated = (
np.dot(dots_keep - rotation_center, rotation_matrix) + rotation_center
)
plt.scatter(
dots_rotated[dots_class == 0, 1],
dots_rotated[dots_class == 0, 0],
color=color_1 if not white else "w",
marker="o",
s=s,
alpha=alpha,
linewidths=linewidths,
)
plt.scatter(
dots_rotated[dots_class == 1, 1],
dots_rotated[dots_class == 1, 0],
color=color_0 if not white else "w",
marker="s",
s=s,
alpha=alpha,
linewidths=linewidths,
)
# Hide axes
plt.axis("off")
return fig
fig = draw_S(figsize=(2, 2))
# Save the figure
plt.savefig(
"skada_logo.svg",
dpi=300,
)
plt.savefig(
"skada_logo.pdf",
dpi=300,
)
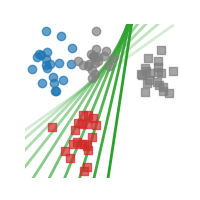
fig = draw_S(figsize=(6, 2))
fontsize = 85
y_axis = 1.5
plt.text(
10,
y_axis,
r"\bf\textsf{K}",
usetex=True,
fontsize=fontsize,
color="black",
)
plt.text(
17,
y_axis,
r"\bf\textsf{A}",
usetex=True,
fontsize=fontsize,
color="black",
)
plt.text(
23.5,
y_axis,
r"\bf\textsf{D}",
usetex=True,
fontsize=fontsize,
color=color_1,
)
plt.text(
30.5,
y_axis,
r"\bf\textsf{A}",
usetex=True,
fontsize=fontsize,
color=color_0,
)
# plt.tight_layout()
# Save the figure
plt.savefig(
"skada_logo_full.svg",
dpi=300,
bbox_inches="tight",
)
plt.savefig(
"skada_logo_full.pdf",
dpi=300,
bbox_inches="tight",
)

fig = draw_S(figsize=(6, 2), white=True)
fontsize = 85
y_axis = 1.5
plt.text(
10,
y_axis,
r"\bf\textsf{K}",
usetex=True,
fontsize=fontsize,
color="w",
)
plt.text(
17,
y_axis,
r"\bf\textsf{A}",
usetex=True,
fontsize=fontsize,
color="w",
)
plt.text(
23.5,
y_axis,
r"\bf\textsf{D}",
usetex=True,
fontsize=fontsize,
color="w",
)
plt.text(
30.5,
y_axis,
r"\bf\textsf{A}",
usetex=True,
fontsize=fontsize,
color="w",
)
# Save the figure
plt.savefig("skada_logo_full_white.svg", transparent=True)
plt.savefig("skada_logo_full_white.pdf", transparent=True)

Total running time of the script: (0 minutes 1.455 seconds)